電漿量測技術
摘要:電漿製程是現今半導體元件製造過程中極為重要的一環,隨著元件尺寸不斷縮小,使用材料多元化,對於製程技術與設備開發所面臨的挑戰也就更加嚴苛,有效掌握製程腔體電漿特性除了有助於深入了解製程中所發生的諸多物理機制及化學反應,更能提供設備開發者正確資訊減少錯誤嘗試機率。本文將針對常用之電漿診斷工具包含蘭牟爾探針及電漿光譜量測進行介紹。
Abstract:Plasma process plays a crucial role in current semiconductor manufacturing. As the component size continues to decrease and materials used become diversified, the challenge faced by the process and equipment development are more severe. Thus, acquisition of plasma characteristics in the process chamber not only provides a deep understanding on physical mechanism and chemical reaction, but also provides correct information to the equipment builders so that trial-and-error attempt can be minimized. This article will focus on plasma diagnosis tools, including introduction of Langmuir probe and plasma spectroscopy measurement.
關鍵詞:電漿量測、蘭牟爾探針、放射光譜
Keywords:Plasma diagnostic, Langmuir probe, Optical emission spectroscopy
前言
電漿腔體中最具影響的應屬電子特性參數,氣體之解離、游離等諸多反應均由腔體內電子密度與溫度所決定,因此電子相關特性之量測極為重要。在各種電漿量測工具中,以侵入式的蘭牟爾探針最能提供完整之電子溫度、密度與能量分佈函數等資訊。而在非侵入式的量測工具中,則以電漿放射光譜最常被使用,可量測電漿中物種成份及其濃度之變化。
蘭牟爾探針
蘭牟爾探針雖然發展得很早(Langmuir 及Mott-Smith於1920年代所發表)[1-3],然而到現在仍是電漿量測技術中極為重要的工具之一。藉由量測一置於電漿中之金屬電極上所施加的直流電壓及相對應所收集到的電流量,也就是熟知的電流-電壓曲線(I-V curve),經由合適的理論模型分析,即可獲知包括電漿電位(plasma potential, Vp)、浮動電位(floating potential, Vf)、電漿密度(plasma density, n)、電子溫度(electron temperature, Te)、電子能量分佈(Electron Energy Distribution Function, EEDF)及機率函數(Electron Energy Probability Function, EEPF)等重要特性參數。同時藉由改變探針所在位置即可量測空間中之電漿參數分佈情形。這對於了解電漿特性亦或者調整製程參數時,可提供極有價值之參考資訊。
1.電流-電壓曲線[4-7]
常見之蘭牟爾探針多使用柱狀結構(cylindrical probe),如圖1所示,長度d半徑a之柱狀探針其外圍鞘層(plasma sheath)厚度為s,假設電漿中僅存在電子及正離子兩種帶電粒子,探針所收集到的總電流包含有離子電流與電子電流兩部份:
I=Ie+Ii
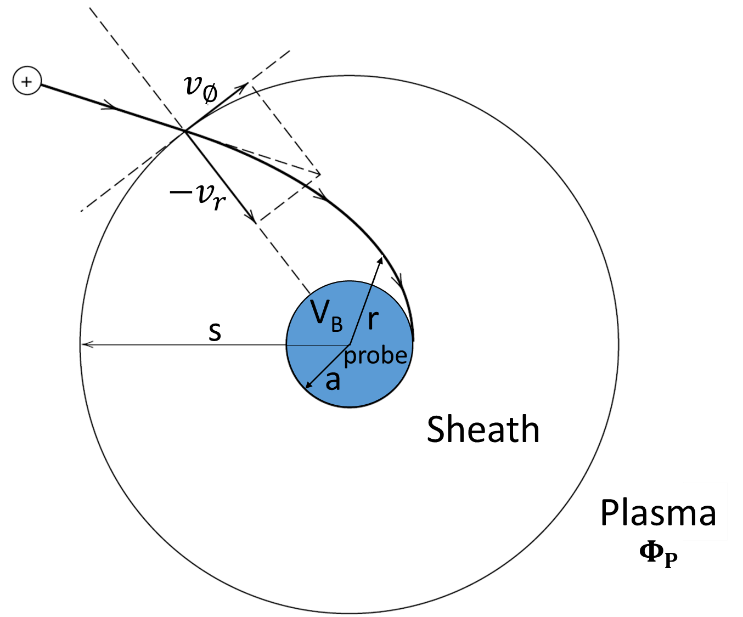
圖1 圓柱形探針截面與離子軌跡[4]
而收集到的電子及離子電流的大小與探針上所施加的電壓VB有關,圖2為一般圓柱型探針所收集到電流電壓曲線(I-V curve)圖。首先考慮當探針電壓遠小於電漿電位(VB<<ΦP)的情況,此時電子受探針上負電壓所排斥,探針僅收集到離子飽和電流Ii,sat。考慮位於鞘層邊緣之離子速度分量分別為vr及v'Φ,進入鞘層最後被探針所收集,速度分量分別為v'r及v'Φ,假設過程中沒有與其他粒子發生碰撞(collisionless sheath),考慮能量與角動量守恆關係:
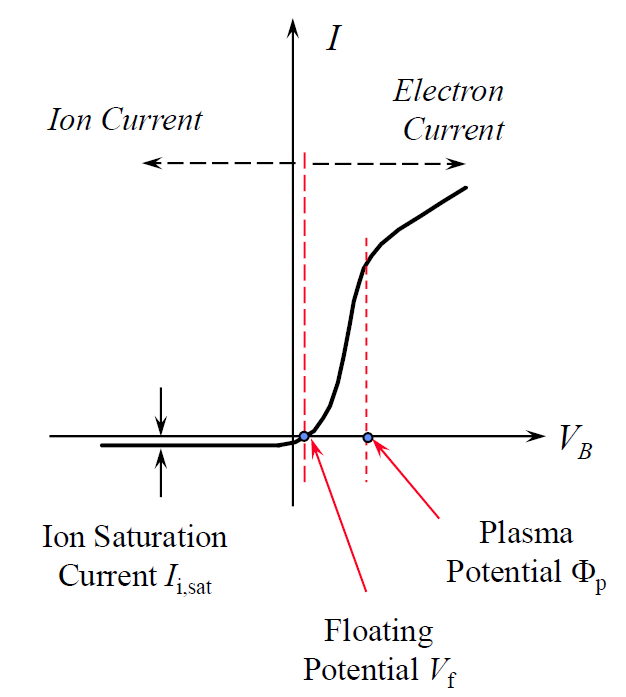
圖2圓柱型探針電流電壓曲線(I-V curve)
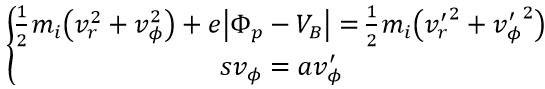 (1)
(1)
其中,mi為離子質量,Φp及VB分別為電漿電位及探針上所施加之電壓值,當離子碰觸到探針表面時,vr' 2=0,則可計算出極限角速度vϕ0,而唯有|vϕ | ≤vϕ0之離子始能到達探針表面被收集到
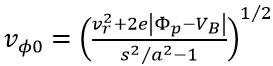 (2)
(2)
探針上所收集到的離子電流可經由積分鞘層表面所有速度及方向之離子而得
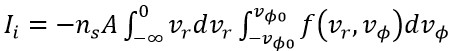 (3)
(3)
假設離子速度分佈為等向性馬克斯威爾分佈
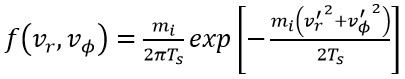 (4)
(4)
在探針電壓遠小於電漿電位時的條件下,a ⁄ s << 1,且vr2 << e | Φp - VB | ⁄mi ,則式(2)可改寫成
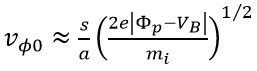 (5)
(5)
將式(4)及(5)代入式(3)可得離子飽和電流
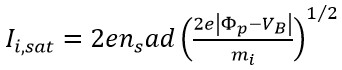 (6)
(6)
其中,ns是鞘層邊緣之離子(電漿)密度,與主電漿區(bulk plasma)電漿密度n0的關係為ns=n0 e-ϕP ⁄ Te ≈ 0.61n0。式(6)取平方之後,由其斜率即可求得離子(電漿)密度:
 (7)
(7)
當探針電壓接近電漿電位(VB ≤ VP)的情況時,探針電流即須要考慮電子電流的收集部分,由於此電壓範圍探針同時會收集到離子及電子電流,因此,常稱之為過渡區。同樣假設電子速度呈馬克斯威爾分佈,經推導可得
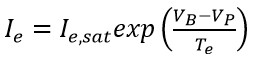 (8)
(8)
其中,為當探針電壓等於電漿電位(VB=VP)時,電子電流及達到飽和狀態,稱之為電子飽和電流,而,為電子平均速度。
根據式(8),電子溫度Te可由電流電壓曲線轉折區域曲自然對數之斜率來求得:
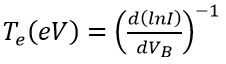 (9)
(9)
而電子能量分佈函數EEDF(electron energy distribution function)以及電子能量機率函數EEPF(electron energy probability function)則可經由電子電流二次微分求得:
…本文未結束
更完整的內容 歡迎訂購 2021年10月號 463期
機械工業雜誌‧每期240元‧一年12期2400元
我要訂購